前言
Hough变换是实现边缘检测的一种有效方法,其基本思想是将测量空间的一点变换到参量空间的一条曲线或曲面,而具有同一参量特征的点变换后在参量空间中相交,通过判断交点处的积累程度来完成特 征曲线的检测。
1 原理
保罗·哈夫于1962年提出了Hough变换法,并申请了专利。该方法 将图像空间中的检测问题转换到参数空间,通过在参数空间里进行简单的累加统计完成检测任务,并用大多数边界点满足的某种参数形式来描述图像的区域边界曲线。这种方法对于被噪声干扰或间断区域边界的图像具有良好的容错性。Hough变换最初主要应用于检测图像空间中的直线,最早的直线变换是在两个笛卡儿坐标系之间进行的,这给检测斜率无穷大的直线带来了困难。1972年,杜达(Duda)将变换形式进行了转化,将数据空间中的点变换为$ρ-θ$参数空间中的曲线,改善了其检测直线的性能。该方法被不断地研究和发展,在图像分析、计算机视觉、模式识别等领域得到了非常广泛的应用,已经成为模式识别的一种重要工具。
直线的方程可由下面式子表示:
其中,$k$和$b$分别是斜率和截距。现在将$y=kx+b$转换成$b=-xk+y$,因为$k$和$b$都是确定值所以在$x-y$平面上的一条线在$k-b$平面上代表一个点。
反过来在$k-b$平面上的一条直线$b=-xk+y$在$x-y$平面上代表一个点,因为此时$x$和$y$在直线$b=-xk+y$中分别是斜率和截距为定值。
其次是过$x-y$平面上的某一点($x_0$,$y_0$) 的所有直线的参数都满足方程$y_0=kx_0+b$。即过$x-y$平面上点($x_0$,$y_0$)的一族直线在参数$k-b$平面上对应于一条直线。同样的道理将该族直线$y_0=kx_0+b$转变到$k-b$平面上有$b=-x_0k+y_0$,此时斜率($-x_0$)和斜距($y_0$)固定,$b$为$k$的函数,所以在$k-b$平面上对应于一条直线。
有了上面的知识,再来看看在$x-y$平面上三点共线是怎么等效到到$k-b$平面的。
可以看出如果笛卡尔坐标系的点共线,这些点在霍夫空间对应的直线交于一点:这也是必然,共线只有一种取值可能。再来考虑特殊情况,当三点共线恰好垂直$x$轴呢?此时直线的斜率$k$为无穷大,$y=kx+b$形式的直线方程无法表示$x=c$($c$为常数)形式的直线。所以在实际应用中,一般采用距离和角度参数方程来表示如下:
其中,$ρ$为原点到直线的垂直距离,$θ$为$ρ$与$x$轴的夹角,转换过程如下,注意的是这个并不是极坐标表达式,只是形式写起来跟极坐标的形式是一样的。这是因为$ρ$和$θ$都是固定的,对应唯一的直线,而如果是极坐标,那其他对的$ρ$和$θ$也会满足这一直线。
根据$ρ=xcosθ+ysinθ$,直线上不同的点在参数空间中被变换为一族相交于$p$点的正弦曲线,因此可以通过检测参数空间中的局部最大值$p$点,来实现$x-y$坐标系中直线的检测。
2 算法流程
①将参数空间量化成$m×n$($m$为$θ$的等份数,$n$为$ρ$的等份数)个单元,并设置累加器矩阵$Q[m×n]$;
②给参数空间中的每个单元分配一个累加器$Q$($θ_i$,$p_j$)($0<i<m-
1$, $0<j<n-1$),并把累加器的初始值置为零;
③将直角坐标系中的各点($x_k$,$y_k$)($k=1$,$2$,…,$s$,$s$为直角坐 标系中的点数)代入式$ρ=xcosθ+ysinθ$,然后将$θ_0~θ_{m-1}$也都代入其中,分别计算出相应的值$p_j$;
④在参数空间中,找到每一个($θ_i$,$p_j$)所对应的单元,并将该 单元的累加器加1,即$Q$($θ_i$,$p_j$) $=$ $Q$($θ_i$,$p_j$) $+1$,对该单元进行一次投票;
⑤待$x-y$坐标系中的所有点都进行运算之后,检查参数空间的累加 器,必有一个出现最大值,这个累加器对应单元的参数值作为所求直线的参数输出。当然你可以指定一个阈值,就是投票数达到多少就可以认定为一条直线,这样就可以一次性输出多条直线。
例子: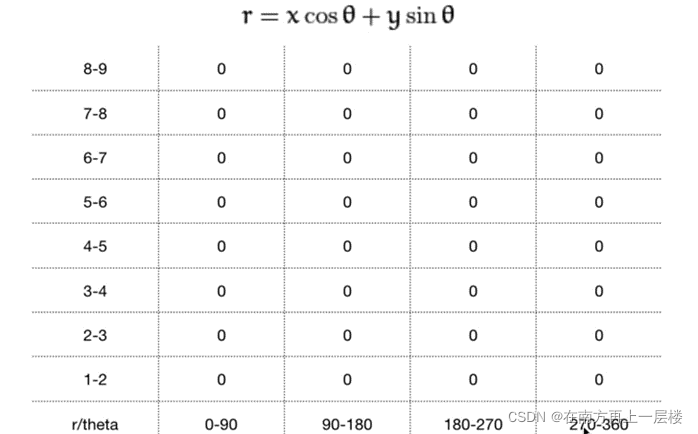
将$r$($p$)分成了9份,区间是[0,9],$r$一定是取有效值,因为我们的图像的最长直线就是其对角线;然后将$θ$以90°为步长分成了4个区间,当然你可以分成你想要的$θ$区间。然后开始遍历 Canny 图像(很关键,我们在利用霍夫变换进行直线检测时,要先对图像进行边缘检测)。
遇到黑点直接跳过,我们只关注白点。然后将每个白点的坐标($x_0$,$y_0$)和四个角度$θ$($θ_1=90°$,$θ_2=180°$,$θ_3=270°$,$θ_4=360°$)带入到$r=xcosθ+ysinθ$中,得到对应的$r_1$,$r_2$,$r_3$,$r_4$,根据这些$r$值在对应区间进行投票。不断重复上述步骤直至图像遍历完毕。就可以根据$r$的投票数来确定直线。
3 优缺点
霍夫变换是一种全局性的检测方法,具有极佳的抗干扰能力,可 以很好地抑制数据点集中存在的干扰,同时还可以将数据点集拟合成多条直线。但是,霍夫变换的精度不容易控制,参数的微变就可能影响效果的大幅度变化,因此,不适合对拟合直线的精度要求较高的实际问题。同时,它所要求的巨大计算量使其处理速度很慢,从而限制了它在实时性要求很高的领域的应用