Z.H.Chen's Blog
0%

对含有奇异值和高斯噪声的数据进行处理

发表于 分类于 Valine：
92 1 分钟

分别用平均滑动窗口、指数滑动窗口、SG滤波法对含有奇异值和高斯噪声的两列数据进行去奇异值和降噪，最终拟合曲线推测函数表达式。去噪方法理论知识参考
对第一列数据：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
import matplotlib.pyplot as plt
import numpy as np
from scipy import optimize
import scipy.io as scio
%matplotlib
#防止中文乱码
plt.rcParams["font.sans-serif"] = ["Simhei"]
plt.rcParams["axes.unicode_minus"] = False
data = scio.loadmat('2 data_preprocess_practice.mat')

yy3 = data["yy3"]
x = np.arange(0, 20001, 1)
#去除奇异值
def Noise_reduction(data_col) :
    lst = []
    i = 0
    #此处用的是3sigema的方法
    while i + 12 < 20001 :
        lst1 = data_col[i : i + 12]
        mean = np.mean(lst1)
        std = np.std(lst1)
        for value in lst1 :
            if (value - mean) >= -3 * std and (value - mean) <= 3 * std :
                lst.append(value)
        i += 12
        lst1 = []
    return lst

#平均滑动去噪
#滑动平均法适用于，噪声的均值为0，真实值变化不大或线性变化的场景
def Average_sliding_denoising(arr, window_size) :
    #对数组进首尾扩展，以滑动窗口可以处理到首尾点，思想与图片滤波算子相似
    New_arr = arr[ : ]
    window_size = (window_size - 1) // 2
    for step in range(window_size) :
        arr.insert(step, sum(arr[ : window_size]) / window_size)
        arr.insert(len(arr) - step, sum(arr[len(arr) - window_size : len(arr)]) / window_size)
    for i in range(window_size, len(arr) - window_size) :
        New_arr[i - window_size] = (sum(arr[i - window_size : i + window_size + 1])) / (2 * window_size + 1)
    return New_arr

#指数平均滑动去噪
#当误差不受观测值大小影响的话，指数滑动平均比滑动平均好；当误差随观测值大小变化时，滑动平均比指数滑动平均更好。
def Exponential_sliding_denoising(arr, weight = 0.01) :
    for i in range(1, len(arr)) :
        arr[i] = weight * arr[i] + (1 - weight) * arr[i - 1]
    return arr

#Savitzky-Golay平滑去噪
#SG滤波法对于数据的观测信息保持的更好，在一些注重数据变化的场合会比较适用。
def create_x(size, rank):
    x = []
    for i in range(2 * size + 1):
        m = i - size
        row = [m ** j for j in range(rank)]
        x.append(row) 
    x = np.mat(x)
    return x

def Savgol_Denosing(arr, window_size, rank) :
    New_arr = arr[ : ]
    m = (window_size - 1) // 2
    # 处理边缘数据，用边缘值首尾增加m个首尾项
    for step in range(m) :
        arr.insert(step, arr[0])
        arr.insert(len(arr) - step, arr[len(arr) - 1])
    # 创建X矩阵
    X = create_x(m, rank)
    # 计算加权系数矩阵B
    B = (X * (X.T * X).I) * X.T
    #只用更新第m个点，因此只需取B系数矩阵的第m行即可
    A0 = B[m].T
    # 计算平滑修正后的值
    narr = []
    for i in range(len(New_arr)):
        y = [arr[i + j] for j in range(window_size)]
        y1 = np.mat(y) * A0
        y1 = float(y1)
        narr.append(y1)
    return narr

#可视化不同去噪方法的效果
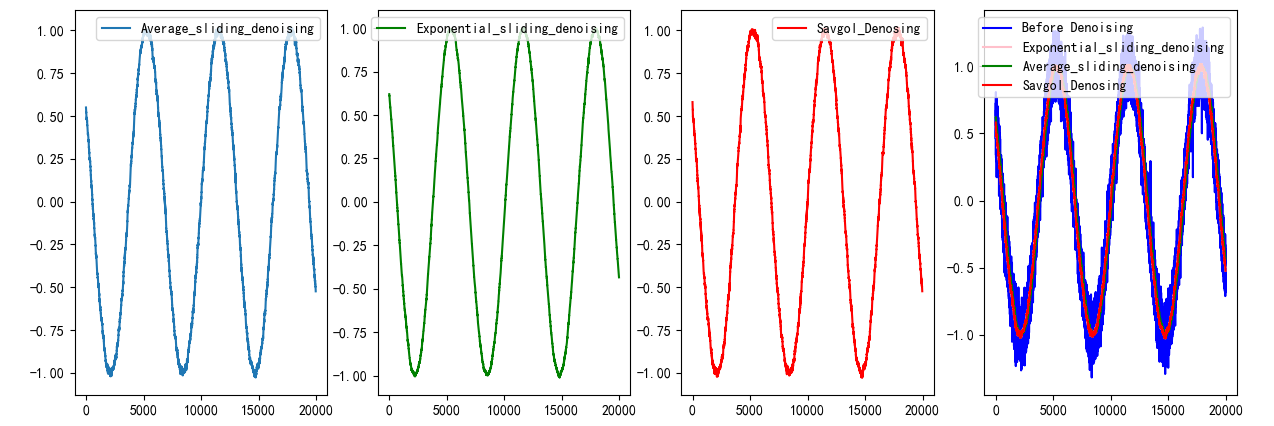
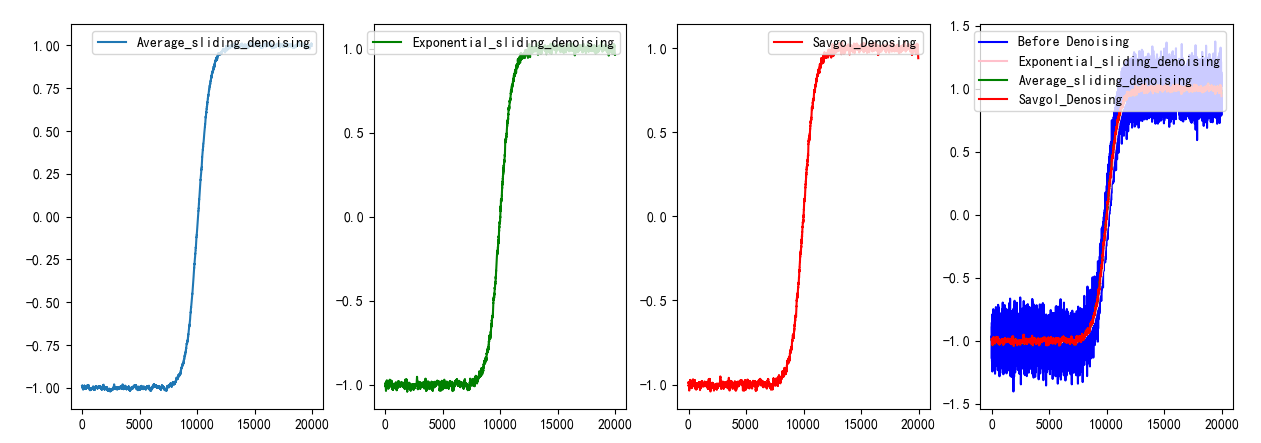
def Mapping(lst, arr, arr1, arr2) :
    x = np.array(list(range(0, len(arr), 1)))
    fig = plt.figure(figsize=(15, 5))
    fig.set(alpha = 0.2)
    plt.subplot2grid((1,4), (0, 0))
    plt.plot(x, arr, label = 'Average_sliding_denoising')
    plt.legend(loc = 1)
    plt.subplot2grid((1, 4), (0, 1))
    plt.plot(x, arr1, 'g-', label = 'Exponential_sliding_denoising')
    plt.legend(loc = 1)
    plt.subplot2grid((1, 4), (0, 2))
    plt.plot(x, arr2, 'r-', label = 'Savgol_Denosing')
    plt.legend(loc = 1)
    plt.subplot2grid((1, 4), (0, 3))
    plt.plot(x, lst, 'b-', x, arr, 'pink', x, arr1, 'g', x, arr2, 'r')
    plt.legend(['Before Denoising', 'Exponential_sliding_denoising', 'Average_sliding_denoising', 'Savgol_Denosing'], loc = 1)
    plt.show()

#小结，单纯从可视化效果来看，指数平均化动的效果是最好的
    
#数据重新拟合，推测函数
def Polynomial_fitting(lst) :
    x1 = np.arange(0, len(lst), 1).astype(float)
    z1 = np.polyfit(x1, lst, 11)
#     print(np.poly1d(z1))
    x_points = np.linspace(0, 19973, 19973)
    y_point = np.polyval(z1, x_points)
    fig1 = plt.figure()
    plt.plot(x1, lst, x_points, y_point, 'r')
    plt.legend(['Before fitting', 'After fitting'], loc = 1)
    plt.show()


data_col1 = []
data_col2 = []
for line in yy3 :
    data_col1.append(line[0])
    data_col2.append(line[1])

data_col1 = np.array(data_col1)
data_col2 = np.array(data_col2)

lst1 = Noise_reduction(data_col1)
lst1_A = Average_sliding_denoising(Noise_reduction(data_col1), 61)
lst1_E = Exponential_sliding_denoising(Noise_reduction(data_col1))
lst1_S = Savgol_Denosing(Noise_reduction(data_col1), 59, 2)
Mapping(lst1, lst1_A, lst1_E, lst1_S)
Polynomial_fitting1(lst1_A)

效果：
在这里插入图片描述

对第二列数据：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def Polynomial_fitting2(lst) :
    x1 = np.arange(0, len(lst), 1).astype(float)
    z1 = np.polyfit(x1, lst, 50)
    x_points = np.linspace(0, 19973, 19973)
    y_point = np.polyval(z1, x_points)
    fig1 = plt.figure()
    plt.plot(x1, lst, x_points, y_point, 'r')
    plt.legend(['Before fitting', 'After fitting'], loc = 1)
    plt.show()
lst2 = Noise_reduction(data_col2)
lst2_A = Average_sliding_denoising(Noise_reduction(data_col2), 61)
lst2_E = Exponential_sliding_denoising(Noise_reduction(data_col2))
lst2_S = Savgol_Denosing(Noise_reduction(data_col2), 59, 2)
Mapping(lst2, lst2_E, lst2_A, lst2_S)
Polynomial_fitting2(lst2_A)

效果：
在这里插入图片描述