Z.H.Chen's Blog
0%

对抗攻击

发表于 分类于 ， Valine：
2.3k 4 分钟

前言

  在人工智能带来的风险中，对抗攻击就是重要风险之一。攻击者可以通过各种手段绕过，或直接对机器学习模型进行攻击达到对抗目的，使我们的模型失效或误判。如果类似攻击发生在无人驾驶、金融AI等领域则将导致严重后果。所以，需要未雨绸缪，认识各种对抗攻击，并有效地破解各种对抗攻击。

1 原理

  对抗攻击最核心的手段就是制造对抗样本去迷惑模型，比如在计算机视觉领域，攻击样本就是向原始样本中添加一些人眼无法察觉的噪声，这些噪声不会影响人类识别，但却很容易迷惑机器学习模型，使它做出错误的判断。如下图所示，在雪山样本中增加一些噪声，结果分类模型就把它视为狗了。
在这里插入图片描述
  机器学习算法的输入形式为数值型向量（Numeric Vectors）。通过设计 一种特别的输入以使模型输出错误的结果，这便被称为对抗性攻击。
  由于机器学习算法的输入形式是一种数值型向量（Numeric Vectors）， 所以攻击者就会通过设计一种有针对性的数值型向量从而让机器学习模型做 出误判，这便被称为对抗性攻击。和其他攻击不同，对抗性攻击主要发生在构造对抗性数据的时候，之后该对抗性数据就如正常数据一样输入机器学习模型并得到欺骗的识别结果。

2 攻击方式

2.1 针对模型的攻击

2.1.1 白盒攻击

  攻击者能够获知机器学习所使用的算法，以及算法所使用的参数。攻击者在产生对抗性攻击数据的过程中能够与机器学习的系统有所交互。

2.1.2 黑盒攻击

  攻击者并不知道机器学习所使用的算法和参数，但攻击者仍能与机器学习的系统有所交互，比如可以通过传入任意输入观察输出，判断输出。

2.2 针对输出的攻击

2.2.1 无目标攻击

  对于一张图像，生成一个对抗样本，使得标注系统在其上的标注与原标 注无关，即只要攻击成功就好，而对抗样本的最终属于哪一类不做限制。

2.2.2 有目标攻击

  对于一张图像和一个目标标注句子，生成一个对抗样本，使得标注系统 在其上的标注与目标标注完全一致，即不仅要求攻击成功，还要求生成的对抗样本属于特定的类。

3 对抗样本生成方式

  快速梯度符号法（FGSM ）攻击是一种以错误分类为目标的白盒攻击。这种攻击非常强大，但也很直观。它旨在通过利用神经网络的学习方式梯度来攻击神经网络。其训练目标是最大化损失函数 $J(x^,y)$以获取对抗样本$x^$，其中$J$是分类算法中衡量分类误差的损失函数，通常取交叉熵损失。最大化$J$即使添加噪声后的样本不再属于$y$类，由此则达到 了下图所示的目的。
在这里插入图片描述
其中$x^*=x+ε·sign(∇_xJ(x,y))$，$sign()$是符号函数，括号里面是损失函数对$x$的偏导，$ε$表示对图片的扰动程度。从图中，$x$是正确分类为“熊猫”的原始输入图像，$y$模型参数$(x,\theta)$下的真实标签，$J(θ,x,y)$是用于训练网络的损失。攻击将梯度反向传播回输入数据以计算$∇_xJ(θ,x,y)$，然后，它通过一小步调整输入数据（$ε$，0.007在上图中）在方向$sign(∇_xJ(θ,x,y))$上使损失最大化。添加噪声之前，原始图像有 $0.557$ 可能被认为是一只熊猫，添加噪声 后，这张图像有 $0.993$ 的可能认为是一种长臂猿。

4 实例

  本次实例受到攻击的模型 MNIST 数据集分类的模型。可以训练并保存自己的 MNIST 模型，也可以从https://drive.google.com/drive/folders/1fn83DF14tWmit0RTKWRhPq5uVXt73e0h下载预训练模型。开始之前要先介绍一下重要的参数 $epsilons$ ：用于运行的 $epsilon$ 值列表。在列表中保留 0 很重要，因为它代表了原始测试集上的模型性能。此外，直观地说，我们预计 $epsilon$ 越大，扰动越明显，但在降低模型精度方面攻击越有效。由于这里的数据范围是[0，1]，任何 $epsilon$ 值不应超过 1。下面是攻击后的图片计算公式：

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
import torchvision
import torchvision.transforms as transform
import matplotlib.pyplot as plt
from torch.utils.data import DataLoader

#设置gpu
device = "cuda" if torch.cuda.is_available() else "cpu"
#数据下载
dataset = torchvision.datasets.MNIST(
    root = 'data',
    train = False,
    download = True,
    #将PIL类型转成tensor
    transform = transform.Compose([
        transform.ToTensor()
    ])
)
test_loader = DataLoader(dataset, batch_size = 1, shuffle = True)
#设置不同的干扰程度
epsilons = [0, .05, .1, .15, .2, .25, .3]

#模型
class Net(nn.Module) :
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(1, 10, kernel_size = 5)
        self.conv2 = nn.Conv2d(10, 20, kernel_size = 5)
        self.dropout = nn.Dropout2d()
        self.fc1 = nn.Linear(320, 50)
        self.fc2 = nn.Linear(50, 10)

    def forward(self, x):
        x = F.relu(F.max_pool2d(self.conv1(x), 2))
        x = F.relu(F.max_pool2d(self.dropout(self.conv2(x)), 2))
        x = x.view(-1, 320)
        x = F.relu(self.fc1(x))
        #传入self.training参数使得训练时使用dropout层，测试时不用
        x = F.dropout(x, training = self.training)
        x = self.fc2(x)
        return F.log_softmax(x, dim=1)

model = Net().to(device)
#下载预训练好的参数
model.load_state_dict(torch.load('lenet_mnist_model.pth', map_location = 'cpu'))
#切换到训练模式
model.eval()

#就算攻击后的图片，如公式（1）所示
def fgsm_attack(image, epsilon, data_grad) :
    #sign（）函数返回数值的符号，如果为正数返回1，如果为负数返回-1.否则返回0
    sign_data_grad = torch.sign(data_grad)
    attack_image = image + epsilon * sign_data_grad
    #因为经过上步骤之后，图片的像素值可能不再[0， 1]区间，所以要限制到[0, 1]之间
    return torch.clamp(attack_image, 0, 1)

def t(model, epsilon, test_loader) :
    #统计被攻击后依然分类正确的图片，也即攻击对分类没有影响
    correct = 0
    #记录攻击成功和攻击失败的图片
    adv_examples = []
    for data, label in test_loader :
        data, label = data.to(device), label.to(device)
        #因为要计算输入图片的梯度，所以要使requires_grad参数为True
        data.requires_grad = True
        #输出
        output = model(data)
        #输出的最大值对应的下标就是模型的分类情况
        _, init_pred = torch.max(output, dim = 1)
        #如果分类没有成功，则不必攻击，没有意义
        if init_pred.item() != label.item() :
            continue
        #计算损失值
        loss = F.nll_loss(output, label)
        #梯度清零
        model.zero_grad()
        #反向传播计算梯度
        loss.backward()
        #得到输入图片的梯度值
        data_grad = data.grad.data
        #对图片进行攻击
        attack_data = fgsm_attack(data, epsilon, data_grad)
        #攻击后图片的模型分类输出
        output = model(attack_data)
        #得到分类的种类
        _, final_pred = torch.max(output, dim = 1)
        #如果攻击后的模型预测与未攻击之前的一样，说明攻击失败
        if final_pred.item() == label.item() :
            correct += 1
            #记录攻击失败的攻击前、攻击后的模型预测情况和图片
            if epsilon == 0 and len(adv_examples) < 5 :
                adv_ex = attack_data.squeeze().detach().cpu().numpy()
                adv_examples.append((init_pred.item(), final_pred.item(), adv_ex))

        else :
            #记录攻击成功的攻击前、攻击后的模型预测情况和图片
            if len(adv_examples) < 5:
                adv_ex = attack_data.squeeze().detach().cpu().numpy()
                adv_examples.append((init_pred.item(), final_pred.item(), adv_ex))
    #输出攻击失败的图片占比
    final_acc = correct / float(len(test_loader))
    print("Epsilon: {}\tTest Accuracy = {} / {} = {}".format(epsilon, correct, len(test_loader), final_acc))

    # Return the accuracy and an adversarial example
    return final_acc, adv_examples

accuracies = []
examples = []

# Run test for each epsilon
for eps in epsilons:
    acc, ex = t(model, eps, test_loader)
    accuracies.append(acc)
    examples.append(ex)

#作出在不同的epsilon下攻击失败的图片占比
fig1 = plt.figure()
plt.plot(epsilons, accuracies, 'o-')
plt.xlabel('eps')
plt.ylabel('acc')
plt.xticks(np.arange(0, 0.35, 0.05))
plt.yticks(np.arange(0, 1.1, 0.1))
plt.savefig('acc_Vs_eps.png')
plt.show()

#展示在不同的epsilon情况的具体的攻击情况
cnt = 0
fig2 = plt.figure(figsize = (8, 10))
for i in range(len(epsilons)) :
    for j in range(len(examples[i])) :
        cnt += 1
        plt.subplot(len(epsilons), len(examples[i]), cnt)
        # plt.axis('off')
        plt.xticks([], [])
        plt.yticks([], [])
        if j == 0:
            plt.ylabel(f'eps : {epsilons[i]}', fontsize = 14)
        plt.title(f'{examples[i][j][0]} -> {examples[i][j][1]}')
        plt.imshow(examples[i][j][2], cmap = 'gray')

plt.tight_layout()
plt.savefig('test.png')
plt.show()

$Accuracy$ 和 $epsilon$ 的关系如下 ：
在这里插入图片描述
如前所述，随着 $epsilon$ 的增加，我们预计测试精度会降低。这是因为更大的 $epsilon$ 意味着我们朝着使损失最大化的方向迈出了更大的一步，当 $epsilon$ 仅为 $0.3$ 是精确度就已经降到了 $0.1$ 以下请注意，即使 $epsilon$ 值是线性间隔的，曲线中的趋势也不是线性的。
对抗样本如下：
在这里插入图片描述
随着 $epsilon$ 的增加，测试精度会降低，但扰动变得更容易察觉。实际上，攻击者必须考虑在准确性降低和可感知性之间进行权衡。在上图中，展示了一些在每个 $epsilon$ 值上成功的对抗性示例。绘图的每一行显示不同的 $epsilon$ 值。第一行是 $epsilon=0$ 也就是 $ε=0$ 表示没有扰动的原始“干净”图像的示例。每张图片的标题显示“原始分类 -> 对抗分类”。当 $epsilon=0.15$ 时扰动开始变得明显。然而，在所有情况下，尽管增加了噪音，人类仍然能够识别正确的类别，但机器无法识别。

5 流程图

  上面所实现的攻击过程可以简化成以下流程图：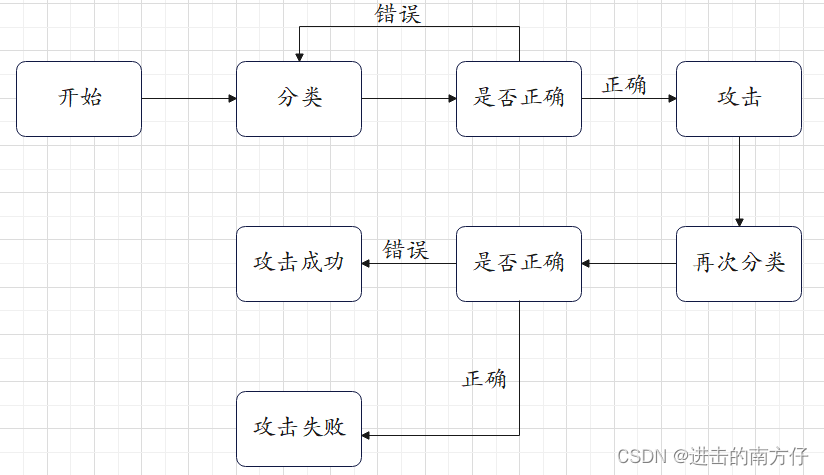
在这里插入图片描述
参考：
https://pytorch.org/tutorials/beginner/fgsm_tutorial.html#fast-gradient-sign-attack