强化学习

# 前言

  强化学习是机器学习领域除有监督学习、无监督学习外的另一个研究分支，它主要利用智能体与环境进行交互，从而学习到能获得良好结果的策略。与有监督学习不同，强化学习的动作并没有明确的标注信息，只有来自环境的反馈的奖励信息，它通常具有一定的滞后性，用于反映动作的“好与坏”。一个完整的强化 学习过程是从一开始什么都不懂，通过不断尝试，从错误或惩罚中学习，最 后找到规律，学会达到目的的方法。
应用领域：
❑ 游戏理论与多主体交互。
❑ 机器人。
❑ 电脑网络。
❑ 车载导航。
❑ 工业物流。

1 原理

  在强化学习问题中，具有感知和决策能力的对象叫作智能体(Agent)，它可以是一段算 法代码，也可以是具有机械结构的机器人软硬件系统。智能体通过与外界的环境进行交互从而完成某个任务，这里的环境(Environment)是指能受到智能体的动作而产生影响，并给出相应反馈的外界环境的总和。对于智能体来说，它通过感知环境的状态(State)而产生决策动作(Action)；对于环境来说，它从某个初始初始状态𝑠1开始，通过接受智能体的动作来动态地改变自身状态，并给出相应的奖励(Reward)信号。
  从概率角度描述强化学习过程，它包含了如下 5 个基本对象：
❑ 状态𝑠 ：反映了环境的状态特征，在时间戳𝑡上的状态记为$𝑠_𝑡$，它可以是原始的视觉图 像、语音波形等信号，也可以是高层抽象过后的特征，如小车的速度、位置等数据，所有的(有限)状态构成了状态空间$S$
❑ 动作𝑎 ：是智能体采取的行为，在时间戳𝑡上的状态记为$𝑎_𝑡$，可以是向左、向右等离散动 作，也可以是力度、位置等连续动作，所有的(有限)动作构成了动作空间$A$
❑ 策略𝜋(𝑎|𝑠)　：代表了智能体的决策模型，接受输入为状态𝑠，并给出决策后执行动作的概率分布𝑝(𝑎|𝑠)，满足 ∑𝜋(𝑎|𝑠) = 1, 𝑎∈𝐴，这种具有一定随机性的动作概率输出称为随机性策略(Stochastic Policy)。特别地，当策略模型总是输出某个动作的概率为 1，其它为 0 时，这种策略模型称为确定性策略(Deterministic Policy)，即 𝑎 = 𝜋(𝑠)
❑ 奖励𝑟(𝑠, 𝑎) ：表达环境在状态𝑠时接受动作𝑎后给出的反馈信号，一般是一个标量值，它 在一定程度上反映了动作的好与坏，在时间戳𝑡上的获得的激励记为𝑟𝑡(部分资料上记为𝑟𝑡+1，这是因为激励往往具有一定滞后性)
❑ 状态转移概率𝑝(𝑠′|𝑠, 𝑎) ：表达了环境模型状态的变化规律，即当前状态𝑠的环境在接受动作𝑎后，状态改变为𝑠′的概率分布，满足 ∑ 𝑝(𝑠′|𝑠, 𝑎) = 1，𝑠′∈𝑆
交互过程可由下图表示：

由交互过程我们得到整个强化学习系统的输入是：
❑ State 为Observation。
❑ Actions 在每个状态下，有什么行动。
❑ Reward 进入每个状态时，能带来正面或负面的回报。
输出是：
❑ Policy 在每个状态下，会选择哪个行动。

  增强学习的任务就是找到一个最优的策略Policy，从而使Reward最多。智能体从环境的初始状态$𝑠_1$开始，通过策略模型𝜋(𝑎|𝑠)采样某个具体的动作$𝑎_1$执行，环境受到动作$𝑎_1$的影响，状态根据内部状态转移模型𝑝(𝑠′|𝑠, 𝑎)发生改变，变为新的状态$s_2$，同时给出智能体的反馈信号：奖励$𝑟_1$，由奖励函数𝑟($𝑠_1$, $𝑎_1$)产生。如此循环交互，直至达到游戏终止状态$𝑎_T$，这个过程产生了一系列的有序数据：𝜏 = $𝑠_1, 𝑎_1, 𝑟_1, 𝑠_2, 𝑎_2, 𝑟_2, ⋯ , 𝑠_𝑇$
  这个序列代表了智能体与环境的一次交换过程，叫做轨迹(Trajectory)，记为𝜏，一次交互过程叫作一个回合(Episode)，𝑇代表了回合的时间戳数(或步数)。有些环境有明确的终止状态(Terminal State)，比如太空侵略者中的小飞机被击中后则游戏结束；而部分环境没有明确的终止标志，如部分游戏只要保持健康状态，则可以无限玩下去，此时𝑇代表∞。增强学习的算法就是需要根据这些样本来 改进策略，从而使得到的样本中的奖励更好。
  强化学习有多种算法，目前比较常用的算法是，通过行为的价值来选取 特定行为的方法，如Q-learning、SARSA，使用神经网络学习的DQN(Deep Q Network)，以及DQN的后续算法，还有直接输出行为的Policy Gradients 等。

2 Q-Learning

2.1 原理

  Q-Learning算法是强化学习中重要且最基础的算法，大多数现代的强化 学习算法，大都是Q-Learning的一些改进。Q-Learning的核心是Q-Table。Q- Table的行和列分别表示State和Action的值，Q-Table的值Q(s,a)衡量当前 States采取行动a的主要依据。

2.2 主要流程

❑ 初始化Q表(初始化为0或随机初始化)
Repeat：
❑ 生成一个在0与1之间的随机数，如果该数大于预先给定的一 个阈值ε，则选择随机动作；否则选择动点依据最高可能性的奖励基于当前状态s和Q表。
❑ 依据上步执行动作。
❑ 采取行动后观察奖励值r和新状态$s_{t+1}$。
❑ 基于奖励值r，利用式下式更新Q表。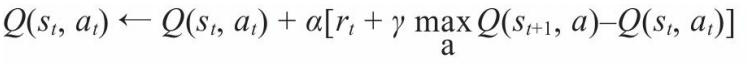
其中α为学习率，γ为折扣率。
❑ 把$s_{t+1}$赋给$s_{t}$

流程图：

2.3 Q函数

 &emps;Q-Learning算法的核心是Q(s,a)函数，其中s表示状态，a表示行动， Q(s,a)的值为在状态s执行a行为后的最大期望奖励值。Q(s,a)函数可以看作一 个表格，每一行表示一个状态，每一列代表一个行动。
  得到Q函数后，就可以在每个状态做出合适的决策了。如当处于$s_1$时， 只需考虑Q($s_1$, :)这些值，并挑选其中最大的Q函数值，并执行相应的动作。

2.4 贪婪策略

  在状态s1时，我们一般是执行根据max(Q($s_1$, : ))中对应的动作a。如果每次都按照这种策略选择行动就有可能局限于现有经验中，不 利于发现更有价值或更新的情况。所以，除根据经验选择行动外，一般还会给主体(Agent)一定的机会或概率，以探索的方式选择行动。 这种平衡“经验”和“探索”的方法又称为ε贪婪(ε-greedy)策略。根据预 先设置好的ε值(该值一般较小，如取0.1)，主体有ε的概率随机行动，有1- ε的概率根据经验选择行动。

2.5 PyTorch实现

  本次用于训练的小游戏是机器人寻找目标星星，如果小机器人接触到五角、星，它就能赢得100分的奖励，如果它接触到小树将得到-100的惩罚。根据奖励进行不断优化最佳路径。

首先要创建游戏并进行交互主要包含了 5 个步骤：
❑ 创建游戏。并返回游戏对象env。
❑ 复位游戏状态。一般游戏环境都具有初始状态，通过调用 env.reset()即可复位游戏状 态，同时返回游戏的初始状态 observation。
❑ 显示游戏画面。通过调用 env.render()即可显示每个时间戳的游戏画面，一般用做测试。在训练时渲染画面会引入一定的计算代价，因此训练时可不显示画面。
❑ 与游戏环境交互。通过 env.step(action)即可执行 action 动作，并返回新的状态observation、当前奖励 reward、游戏是否结束标志 done。通过循环此步骤即可持续与环境交互，直至游戏回合结束。
❑ 销毁游戏。调用 env.close()即可。

class Env(tk.Tk):
    def __init__(self):
        super(Env, self).__init__()
        self.action_space = ['u', 'd', 'l', 'r']
        self.n_actions = len(self.action_space)
        self.title('Q Learning')
        self.geometry('{0}x{1}'.format(HEIGHT * UNIT, HEIGHT * UNIT))
        self.shapes = self.load_images()
        self.canvas = self._build_canvas()
        self.texts = []

    def _build_canvas(self):
        canvas = tk.Canvas(self, bg='white',
                           height=HEIGHT * UNIT,
                           width=WIDTH * UNIT)
        # create grids
        for c in range(0, WIDTH * UNIT, UNIT):  # 0~400 by 100
            x0, y0, x1, y1 = c, 0, c, HEIGHT * UNIT
            canvas.create_line(x0, y0, x1, y1)
        for r in range(0, HEIGHT * UNIT, UNIT):  # 0~400 by 100
            x0, y0, x1, y1 = 0, r, HEIGHT * UNIT, r
            canvas.create_line(x0, y0, x1, y1)

        # 把图标加载到环境中
        self.rectangle = canvas.create_image(50, 50, image=self.shapes[0])
        self.tree1 = canvas.create_image(250, 150, image=self.shapes[1])
        self.tree2 = canvas.create_image(150, 250, image=self.shapes[1])
        self.star = canvas.create_image(250, 250, image=self.shapes[2])

        # 对环境进行包装
        canvas.pack()

        return canvas

    def load_images(self):
        rectangle = PhotoImage(
            Image.open("img/bob.png").resize((65, 65)))
        tree = PhotoImage(
            Image.open("img/tree.png").resize((65, 65)))
        star = PhotoImage(
            Image.open("img/star.jpg").resize((65, 65)))

        return rectangle, tree, star

    def text_value(self, row, col, contents, action, font='Helvetica', size=10,
                   style='normal', anchor="nw"):
        if action == 0:
            origin_x, origin_y = 7, 42
        elif action == 1:
            origin_x, origin_y = 85, 42
        elif action == 2:
            origin_x, origin_y = 42, 5
        else:
            origin_x, origin_y = 42, 77

        x, y = origin_y + (UNIT * col), origin_x + (UNIT * row)
        font = (font, str(size), style)
        text = self.canvas.create_text(x, y, fill="black", text=contents,
                                       font=font, anchor=anchor)
        return self.texts.append(text)

    def print_value_all(self, q_table):
        for i in self.texts:
            self.canvas.delete(i)
        self.texts.clear()
        for i in range(HEIGHT):
            for j in range(WIDTH):
                for action in range(0, 4):
                    state = [i, j]
                    if str(state) in q_table.keys():
                        temp = q_table[str(state)][action]
                        self.text_value(j, i, round(temp, 2), action)

    def coords_to_state(self, coords):
        x = int((coords[0] - 50) / 100)
        y = int((coords[1] - 50) / 100)
        return [x, y]

    def state_to_coords(self, state):
        x = int(state[0] * 100 + 50)
        y = int(state[1] * 100 + 50)
        return [x, y]

    def reset(self):
        self.update()
        time.sleep(0.5)
        x, y = self.canvas.coords(self.rectangle)
        self.canvas.move(self.rectangle, UNIT / 2 - x, UNIT / 2 - y)
        self.render()
        # return observation
        return self.coords_to_state(self.canvas.coords(self.rectangle))

    def step(self, action):
        state = self.canvas.coords(self.rectangle)
        base_action = np.array([0, 0])
        self.render()

        if action == 0:  # up
            if state[1] > UNIT:
                base_action[1] -= UNIT
        elif action == 1:  # down
            if state[1] < (HEIGHT - 1) * UNIT:
                base_action[1] += UNIT
        elif action == 2:  # left
            if state[0] > UNIT:
                base_action[0] -= UNIT
        elif action == 3:  # right
            if state[0] < (WIDTH - 1) * UNIT:
                base_action[0] += UNIT

        # 移动
        self.canvas.move(self.rectangle, base_action[0], base_action[1])
        self.canvas.tag_raise(self.rectangle)
        next_state = self.canvas.coords(self.rectangle)
        # 判断得分条件
        if next_state == self.canvas.coords(self.star):
            reward = 100
            done = True
        elif next_state in [self.canvas.coords(self.tree1),
                            self.canvas.coords(self.tree2)]:
            reward = -100
            done = True
        else:
            reward = 0
            done = False

        next_state = self.coords_to_state(next_state)
        return next_state, reward, done

    # 渲染环境
    def render(self):
        time.sleep(0.03)
        self.update()

Q函数：

class QLearningAgent:
    def __init__(self, actions):
        # 四种动作分别用序列表示：[0, 1, 2, 3]
        self.actions = actions
        self.learning_rate = 0.01
        self.discount_factor = 0.9
        #epsilon贪婪策略取值
        self.epsilon = 0.1
        self.q_table = defaultdict(lambda: [0.0, 0.0, 0.0, 0.0])

    # 采样 <s, a, r, s'>
    def learn(self, state, action, reward, next_state):
        current_q = self.q_table[state][action]
        # 更新Q表
        new_q = reward + self.discount_factor * max(self.q_table[next_state])
        self.q_table[state][action] += self.learning_rate * (new_q - current_q)

    # 从Q-table中选取动作
    def get_action(self, state):
        if np.random.rand() < self.epsilon:
            # 贪婪策略随机探索动作
            action = np.random.choice(self.actions)
        else:
            # 从q表中选择
            state_action = self.q_table[state]
            action = self.arg_max(state_action)
        return action

    @staticmethod
    def arg_max(state_action):
        max_index_list = []
        max_value = state_action[0]
        for index, value in enumerate(state_action):
            if value > max_value:
                max_index_list.clear()
                max_value = value
                max_index_list.append(index)
            elif value == max_value:
                max_index_list.append(index)
        return random.choice(max_index_list)

训练：

env = Env()
agent = QLearningAgent(actions=list(range(env.n_actions)))
#共进行200次游戏
for episode in range(200):
    state = env.reset()
    while True:
        env.render()
        # agent产生动作
        action = agent.get_action(str(state))
        next_state, reward, done = env.step(action)
        # 更新Q表
        agent.learn(str(state), action, reward, str(next_state))
        state = next_state
        env.print_value_all(agent.q_table)
        # 当到达终点就终止游戏开始新一轮训练
        if done:
            break

3 SARSA 算法

  SARSA 算法通过：$𝑄^π(𝑠_𝑡, 𝑎_𝑡)$ ← $𝑄^π(𝑠_𝑡, 𝑎_𝑡)$ + 𝛼(𝑟$(𝑠_𝑡, 𝑎_𝑡)$ + 𝛾$𝑄^π(𝑠_{𝑡+1}, 𝑎_{𝑡+1})$ − $𝑄^π(𝑠_𝑡, 𝑎_𝑡)$方式估计 Q 函数，在轨迹的每一步，只需要$𝑠_𝑡、𝑎_𝑡、𝑟_𝑡、𝑠_{𝑡+1}、𝑎_{𝑡+1}$数据即可更新一次 Q 网络，所以叫做 SARSA 算法(State Action Reward State Action)。SARSA 算法与Q-Leanring算法的不同之处就是在于 Q 表的更新方式的不同。

3.1 主要流程

❑ 获取初始状态s。
❑ 执行上一步选择的行动a，获得奖励r和新状态next_s。
❑ 在新状态next_s，根据当前的Q表，选定要执行的下一行动next_a。
❑ 用r、next_a、next_s，根据SARSA逻辑更新Q表。
❑ 把next_s赋给s，把next_a赋给a。

3.2 PyTorch实现

  SARSA算法与Q-Learning算法的差异是在Q表的更新方式，所以主要修改学习函数。
❑ 修改学习函数：

# 采样 <s, a, r,a',s'>
    def learn(self, state, action, reward,next_action,next_state):
        current_q = self.q_table[state][action]
        # 更新Q表
        new_q = reward + self.discount_factor * (self.q_table[next_state][next_action])
        self.q_table[state][action] += self.learning_rate * (new_q - current_q)

❑ 修改训练代码:

env = Env()
agent = QLearningAgent(actions=list(range(env.n_actions)))
#共进行200次游戏
for episode in range(200):
    state = env.reset()
    action = agent.get_action(str(state))
    while True:
        env.render()
        #获取新的状态、奖励分数
        next_state, reward, done = env.step(action)
        #产生新的动作
        next_action = agent.get_action(str(state))
        # 更新Q表，sarsa根据新的状态及动作获取Q表的值
        #而不是基于新状态对所有动作的最大值
        agent.learn(str(state), action, reward, next_action,str(next_state))
        state = next_state
        action=next_action
        env.print_value_all(agent.q_table)
        # 当到达终点就终止游戏开始新一轮训练
        if done:
            break

github地址：https://github.com/aishangcengloua/MLData/tree/master/PyTorch/ReinforcementLearning

参考文献：
❑ ：Python深度学习基于PyTorch
❑ ：TensorFlow深度学习