自编码器

前言

  目前我们可以通过爬虫等方式获取海量的样本数据𝒙，如照片、语音、文本等，是相对容易的，但困难的是获取这些数据所对应的标签信息，例如机器翻译，除了收集源语言的对话文本外，还需要待翻译的目标语言文本数据。数据的标注工作目前主要还是依赖人的先验知识来完成。因此，面对海量的无标注数据，我们需要从中学习到数据的分布𝑃(𝒙)的算法，而无监督算法模型就是针对这类问题而发展的。特别地，如果算法把𝒙作为监督信号来学习，这类算法称为自监督学习，本博客介绍的自编码器就属于自监督学习范畴。

1 自编码器

1.1 原理

  自编码器是通过对输入$x$进行编码后得到一个低维的向量$z$，然后根据 这个向量还原出输入$x$。通过对比$x$与$\bar{x}$的误差，再利用神经网络去训练使得误差逐渐减小，从而达到非监督学习的目的。结构如下图所示。

  其中我们将数据𝒙本身作为监督信号来指导网络的训练，即希望神经网络能够学习到映射${𝑓_θ}$: $x$ → $x$，我们把网络𝑓𝜃切分为两个部分，前面的子网络尝试学习映射关系：$g_{θ1}$: $x$ → $z$，后面的子网络尝试学习映射关系：$h_{θ2}$：$z$ → $x$。我们把$g_{θ1}$看成一个数据编码(Encode)的过程，作用就是将输入$x$编码成低纬度的隐藏变量$z$，$h_{θ2}$看成一个数据解码(Dncode)的过程，作用是将隐藏变量$z$重塑成高纬度的$x$。编码器和解码器共同完成了输入数据$x$的编码和解码过程，我们把整个网路模型${𝑓_θ}$叫做自动编码器(Auto-Encoder)，如果网络含有多个隐藏层，则称为深度自编码器(Deep Auto-encoder)。
  自编码器的编码器通过编码器压缩得到的隐藏变量$z$重塑$\bar{x}$，我们希望解码器的输出能够完美地或者近似恢复出原来的输入，即$x$约等于$\bar{x}$，则自编码器的损失函数可定义为

$$\begin{aligned} &Minimize ℒ = dist(x, \bar{x})\\ &\bar{x} = h_{θ2}(g_{θ1}(x))\\ \end{aligned}$$

  其中$dist(x, \bar{x})$表示$x$与 $\bar{x}$ 的距离，常见的距离度量函数为欧氏距离(也即均方差):

$$\begin{aligned} &ℒ = \sum_{i}(x - \bar{x})^2\\ \end{aligned}$$

1.2 PyTorch实现图片重塑

1.2.1 Fashion MNIST 数据集

  Fashion MNIST 是一个定位在比 MNIST 图片识别问题稍复杂的数据集，它的设定与MNIST 几乎完全一样，包含了 10 类不同类型的衣服、鞋子、包等灰度图片，图片大小为28 × 28，共 70000 张图片，其中 60000 张用于训练集，10000 张用于测试集。Fashion MNIST 除了图片内容与 MNIST 不一样，其它设定都相同，大部分情况可以直接替换掉原来基于 MNIST 训练的算法代码，而不需要额外修改。由于 Fashion MNIST 图片识别相对于 MNIST 图片更难，因此可以用于测试稍复杂的算法性能。

  在PyTorch中可以直接使用torchvision包进行在线下载。

dataset = datasets.FashionMNIST(root = 'data2',
                        train = False,
                        download = True,
                        transform = transforms.ToTensor())

1.2.2 网络结构

  我们利用编码器将输入图片$x ∈ 𝑅^{784}降维到较低维度的隐藏向量z∈ 𝑅^{20}$，并基于隐藏向量 利用解码器重建图片，自编码器模型如图所示，编码器由 3 层全连接层网络组成，输出节点数分别为 256、128、20，解码器同样由 3 层全连接网络组成，输出节点数分别为 128、256、784。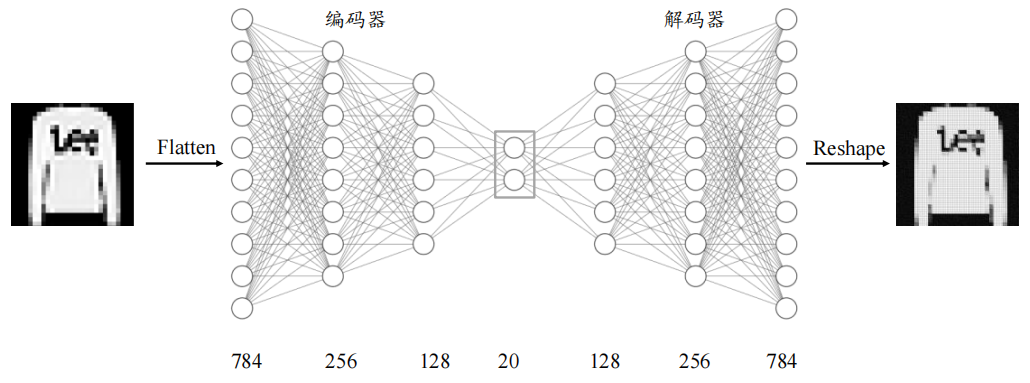

class AE(nn.Module) :
    def __init__(self):
        super(AE, self).__init__()
        self.fc1 = nn.Linear(784, 256)
        self.relu1 = nn.ReLU()
        self.fc2 = nn.Linear(256, 128)
        self.relu2 = nn.ReLU()
        self.fc3 = nn.Linear(128, 20)
        self.fc4 = nn.Linear(20, 128)
        self.relu3 = nn.ReLU()
        self.fc5 = nn.Linear(128, 256)
        self.relu4 = nn.ReLU()
        self.fc6 = nn.Linear(256, 784)

    def Encoder(self, x):
        h1 = self.relu1(self.fc1(x))
        h2 = self.relu2(self.fc2(h1))
        return self.fc3(h2)

    def Decoder(self, z):
        h1 = self.relu3(self.fc4(z))
        h2 = self.relu4(self.fc5(h1))
        return F.sigmoid(self.fc6(h2))

    def forward(self, x):
        z = self.Encoder(x)
        # print(z.shape)
        x_reconst = self.Decoder(z)
        return x_reconst

1.2.3 训练

  自编码器的训练过程与分类器的基本一致，通过误差函数计算出重建向量$\bar{x} 与原始输入向量x$之间的距离。

for epoch in range(MAX_EPOCH) :
    model.train()
    for i, (x, _) in enumerate(data_loader) :
        x = x.to(device)
        optimizer.zero_grad()
        x = x.view(-1, image_size)
        x_reconst = model(x)
        # 重构损失，使用二元分类损失
        reconst_loss = F.binary_cross_entropy(x_reconst, x, size_average=False)

        reconst_loss.backward()
        optimizer.step()

1.2.4 图片重塑

  与分类问题不同的是，自编码器的模型性能一般不好量化评价，尽管ℒ值可以在一定程度上代表网络的学习效果，但我们最终希望获得还原度较高、样式较丰富的重建样本。对于图片来说，一般依赖于人工主观的评估。在这次实践中正确做法应是将数据集划分为训练集和测试集，用测试集来进行图片重塑对比，但我为了方便就直接使用训练集来进行重塑了。

with torch.no_grad() :
    out = model(x)
    #将与原图与重塑图像进行拼接，奇数列为原图像，偶数列为重塑图像
    x_concat = torch.cat([x.view(-1, 1, 28, 28), out.view(-1, 1, 28, 28)], dim = 3)
    save_image(x_concat, os.path.join(samples_dir, f'reconst-{epoch 

  重塑图像如上图，其中奇数列为原图像，偶数列为重塑图像。可以看到，第一个 Epoch 时，图片重建效果较差，图片非常模糊，逼真度较差；随着训练的进行，重建图片边缘越来越清晰，第 100 个 Epoch时，重建的图片效果已经比较接近真实图片。
全部代码：

import os
import torch
import cv2 as cv
import matplotlib.pyplot as plt
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import torchvision.datasets as datasets
from torch.utils.data import DataLoader, Dataset
from torchvision.utils import save_image
from torchvision import transforms

MAX_EPOCH = 100
lr_learning = 0.001
batch_size = 64
image_size = 784
os.makedirs('samples_AE', exist_ok = True)
samples_dir = 'samples_AE'

dataset = datasets.FashionMNIST(root = 'data2',
                        train = False,
                        download = True,
                        transform = transforms.ToTensor())

data_loader = DataLoader(dataset, shuffle = True, batch_size = batch_size, drop_last = True)

class AE(nn.Module) :
    def __init__(self):
        super(AE, self).__init__()
        self.fc1 = nn.Linear(784, 256)
        self.relu1 = nn.ReLU()
        self.fc2 = nn.Linear(256, 128)
        self.relu2 = nn.ReLU()
        self.fc3 = nn.Linear(128, 20)
        self.fc4 = nn.Linear(20, 128)
        self.relu3 = nn.ReLU()
        self.fc5 = nn.Linear(128, 256)
        self.relu4 = nn.ReLU()
        self.fc6 = nn.Linear(256, 784)

    def Encoder(self, x):
        h1 = self.relu1(self.fc1(x))
        h2 = self.relu2(self.fc2(h1))
        return self.fc3(h2)

    def Decoder(self, z):
        h1 = self.relu3(self.fc4(z))
        h2 = self.relu4(self.fc5(h1))
        return F.sigmoid(self.fc6(h2))

    def forward(self, x):
        z = self.Encoder(x)
        # print(z.shape)
        x_reconst = self.Decoder(z)
        return x_reconst

device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model = AE().to(device)
optimizer = optim.Adam(model.parameters(), lr = lr_learning)

for epoch in range(MAX_EPOCH) :
    model.train()
    for i, (x, _) in enumerate(data_loader) :
        x = x.to(device)
        optimizer.zero_grad()
        x = x.view(-1, image_size)
        x_reconst = model(x)
        # 重构损失，使用二元分类损失
        reconst_loss = F.binary_cross_entropy(x_reconst, x, size_average=False)

        reconst_loss.backward()
        optimizer.step()

    with torch.no_grad() :
        out = model(x)
        #将与原图与重塑图像进行拼接，奇数列为原图像，偶数列为重塑图像
        x_concat = torch.cat([x.view(-1, 1, 28, 28), out.view(-1, 1, 28, 28)], dim = 3)
        save_image(x_concat, os.path.join(samples_dir, f'reconst-{epoch + 1}.png'))

img1 = cv.imread('samples_AE/reconst-1.png')
img2 = cv.imread('samples_AE/reconst-50.png')
img3 = cv.imread('samples_AE/reconst-100.png')

images = [img1, img2, img3]
xlabels = ['epoch : 1', 'epoch : 50', 'epoch : 100']
for i in range(3) :
    plt.subplot(1, 3, i + 1)
    plt.imshow(images[i], 'gray')
    plt.axis('off')
    plt.title(xlabels[i])
    plt.tight_layout()
plt.show()

2 自编码器变种

2.1 降噪自编码器(DAE)

  DAE是通过改变重构误差项来获得一个能学到有用信息的自编码器。对于传统的自编码器最小优化目标：

$$\begin{aligned} &θ^∗ = argmin _θ \quad\ dist(ℎθ2(𝑔θ1(x)), x)\\ \end{aligned}$$

  对于这个函数如果模型被赋予过大的容量，损失函数仅仅使得 g ◦ f 学成一个恒等函数。也即网络会简单地复制输入，网络没有学习特征的能力。DAE给网络输入$x$添加采样自高斯分布的噪声$\alpha$：

$$\begin{aligned} &x^\prime = x + \alpha, \alpha∈𝒩(0, var)\\ \end{aligned}$$

则优化目标变成：

$$\begin{aligned} &θ^∗ = argmin _θ \quad\ dist(ℎ_{θ2}(𝑔_{θ1}(x^\prime)), x)\\ \end{aligned}$$

  其中$x^\prime$是被某种噪声损坏的$x$的副本。因此去噪自编码器必须撤消这些损坏，而不是简单地复制输入。

2.2 对抗自编码器(AAE)

  为了能够方便地从某个已知的先验分布中𝑝(𝒛)采样隐藏变量𝒛，方便利用𝑝(𝒛)来重建输 入，对抗自编码器利用额外的判别器网络(Discriminator，简称 D网络)来判定降维的隐藏变量𝒛是否采样自先验分布𝑝(𝒛)。判别器网络的输出为一个属于[0,1]区间的变量，表征隐藏向量是否采样自先验分布𝑝(𝒛)：所有采样自先验分布𝑝(𝒛)的𝒛标注为真，采样自编码器的条件概率𝑞(𝒛|𝒙)的𝒛标注为假。通过这种方式训练，除了可以重建样本，还可以约束条件概率分布𝑞(𝒛|𝒙)逼近先验分布𝑝(𝒛)。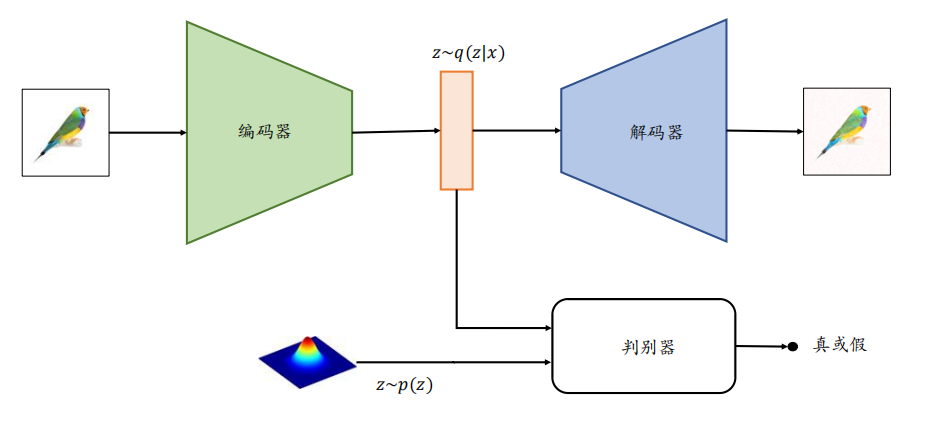

2.3 变分自编码器(VAE)

2.3.1 原理

  自编码器因不能随意产生合理的潜在变量，从而导致它无法产生新的内容。因为潜在变量$z$都是编码器从原始图片中产生的。为解决这一问题，研究人员对潜在空间$z$(潜在变量对应的空间)增加一些约束，使$z$满足正态分布，由此就出现了VAE模型，VAE对编码器添加约束，就是强迫它产生服从单位正态分布的潜在变量。正是这种约束，把VAE和自编码器区分开来。
  从神经网络的角度来看，VAE 相对于自编码器模型，同样具有编码器和解码器两个子网络。解码器接受输入$x$，输出为隐变量$z$；解码器负责将隐变量$z$解码为重建的$x$。不同的是，VAE 模型对隐变量$z$的分布有显式地约束，希望隐变量$z$符合预设的先验分布P($z$)。因此，在损失函数的设计上，除了原有的重建误差项外，还添加了隐变量$z$分布的约束项。也即我们优化目标希望$z$的分布接近于正态分布。度量图像的相似度一般采用交叉熵(如nn.BCELoss)，度量两个分布 的相似度一般采用KL散度(Kullback-Leibler divergence)。这两个度量的和 构成了整个模型的损失函数。变分自编码器的结构如下：

模块1：把输入样本$x$通过编码器输出两个m维向量(mu、log_var)，这两个向量是潜在空间(假设满足正态分布)的两个参数(相当于均值和方差)。
模块2：从标准正态分布N(0,I)中采样 一个ε。
模块3：使得$z$=mu+exp(log_var)*ε。
模块4：$z$通过解码器生成一个样本$\bar{x}$。

损失函数的具体代码如下，推导过程：https://arxiv.org/pdf/1606.05908.pdf

# 定义重构损失函数及KL散度 
reconst_loss = F.binary_cross_entropy(x_reconst, x, size_average=False)
kl_div = - 0.5 * torch.sum(1 + log_var - mu.pow(2) - log_var.exp()) 
#两者相加得总损失 loss= reconst_loss+ kl_div

2.3.2 VAE图片生成

  此次我们基于 VAE 模型实战MNIST手写数字图片的重建与生成。输入为 MNIST手写数字图片向量，经过 3 个全连接层后得到隐向量𝐳的均值与方差，分别用两个输出节点数为 20 的全连接层表示，FC2 的 20 个输出节点表示 20 个特征分布的均值向量，FC3 的 20 个输出节点表示 20 个特征分布的取log后的方差向量。采样获得长度为 20 的隐向量𝐳，并通过 FC4 和 FC5 重建出样本图片。
  VAE 作为生成模型，除了可以重建输入样本，还可以单独使用解码器生成样本。通过从先验分布𝑝(𝐳)中直接采样获得隐向量𝐳，经过解码后可以产生生成的样本。

  此过程的实现与图片的重塑过程相差不大，主要差异在损失函数部分和潜在变量$z$的采样部分。

import cv2 as cv
import numpy as np
import os
import torch
import matplotlib.pyplot as plt
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
import torchvision.datasets as datasets
from torch.utils.data import DataLoader, Dataset
from torchvision.utils import save_image
from torchvision import transforms

MAX_EPOCH = 100
lr_learning = 0.001
batch_size = 64
hidden_size = 400
z_size = 20
image_size = 784
os.makedirs('samples', exist_ok = True)
samples_dir = 'samples'

dataset=datasets.MNIST( root = 'data',
                        train = False,
                        download = True,
                        transform = transforms.ToTensor())

data_loader = DataLoader(dataset, shuffle = True, batch_size = batch_size, drop_last = True)

class VAE(nn.Module) :
    def __init__(self, image_size, hidden_size, z_size):
        super(VAE, self).__init__()
        self.fc1 = nn.Linear(image_size, hidden_size)
        self.relu1 = nn.ReLU()
        self.fc2 = nn.Linear(hidden_size, z_size)
        self.fc3 = nn.Linear(hidden_size, z_size)
        self.fc4 = nn.Linear(z_size, hidden_size)
        self.relu2 = nn.ReLU()
        self.fc5 = nn.Linear(hidden_size, image_size)

    def Encoder(self, x):
        h = self.relu1(self.fc1(x))
        return self.fc2(h), self.fc3(h)

    def Reparameterize(self, mu, Log_var):
        std = torch.exp(Log_var / 2)
        eps = torch.randn_like((std))
        return mu + eps * std

    def Decoder(self, z):
        h = self.relu2(self.fc4(z))
        return F.sigmoid(self.fc5(h))

    def forward(self, x):
        mu, Log_var = self.Encoder(x)
        z = self.Reparameterize(mu, Log_var)
        x_reconst = self.Decoder(z)
        return x_reconst, mu, Log_var

device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model = VAE(image_size, hidden_size, z_size).to(device)
optimizer = optim.Adam(model.parameters(), lr = lr_learning)

for epoch in range(MAX_EPOCH) :
    model.train()
    for i, (x, _) in enumerate(data_loader) :
        x = x.to(device)
        optimizer.zero_grad()
        x = x.view(-1, image_size)
        x_reconst, mu, Log_var = model(x)
        # 计算重构损失和KL散度
        # 重构损失
        reconst_loss = F.binary_cross_entropy(x_reconst, x, size_average=False)
        # KL散度
        kl_div = - 0.5 * torch.sum(1 + Log_var - mu.pow(2) - Log_var.exp())
        loss = reconst_loss + kl_div
        loss.backward()
        optimizer.step()

        # if i % 10 == 0 :
        #     print(f'reconst_loss : {reconst_loss : 0.3f}, kl_div : {kl_div : 0.3f}')

    with torch.no_grad() :
        #图片生成
        z = torch.randn(batch_size, z_size).to(device)
        out = model.Decoder(z).view(-1, 1, 28, 28)
        save_image(out, os.path.join(samples_dir, f'sampled-{epoch + 1}.png'))
        #图片重塑
        out, _, _ = model(x)
        print(x.shape)
        x_concat = torch.cat([x.view(-1, 1, 28, 28), out.view(-1, 1, 28, 28)], dim = 3)
        save_image(x_concat, os.path.join(samples_dir, f'reconst-{epoch + 1}.png'))

img1 = cv.imread('samples/sampled-1.png')
img2 = cv.imread('samples/sampled-50.png')
img3 = cv.imread('samples/sampled-100.png')

img4 = cv.imread('samples/reconst-1.png')
img5 = cv.imread('samples/reconst-50.png')
img6 = cv.imread('samples/reconst-100.png')

images = [img1, img2, img3, img4, img5, img6]
xlabels = ['images sample epoch : 1', 'epoch : 50', 'epoch : 100', 'images reconst epoch : 1', 'epoch : 50', 'epoch : 100']
plt.figure(figsize = (15, 10))
for i in range(6) :
    plt.subplot(2, 3, i + 1)
    plt.imshow(images[i], 'gray')
    plt.axis('off')
    plt.title(xlabels[i])
    plt.tight_layout()
plt.show()

  效果如下，其中重塑图片中奇数列是原图，偶数列为重塑图像。由潜在空间点$z$生成的图像随着epoch的增加是越来越清晰的。

参考
《TensorFlow深度学习》
《Python深度学习基于PyTorch》