1 什么是图

图是一种数据结构，可用于对对象之间的层次结构和关系进行建模。它由一组节点和一组边组成。节点表示单个对象，而边表示这些对象之间的关系。注意：可能在不同的文献中节点也被称作顶点，它们指同一个意思。
如果图中的边可以通过双向遍历，则是无向图(undirected)，如果只能通过一个方向进行遍历，则是有向图(undirected)。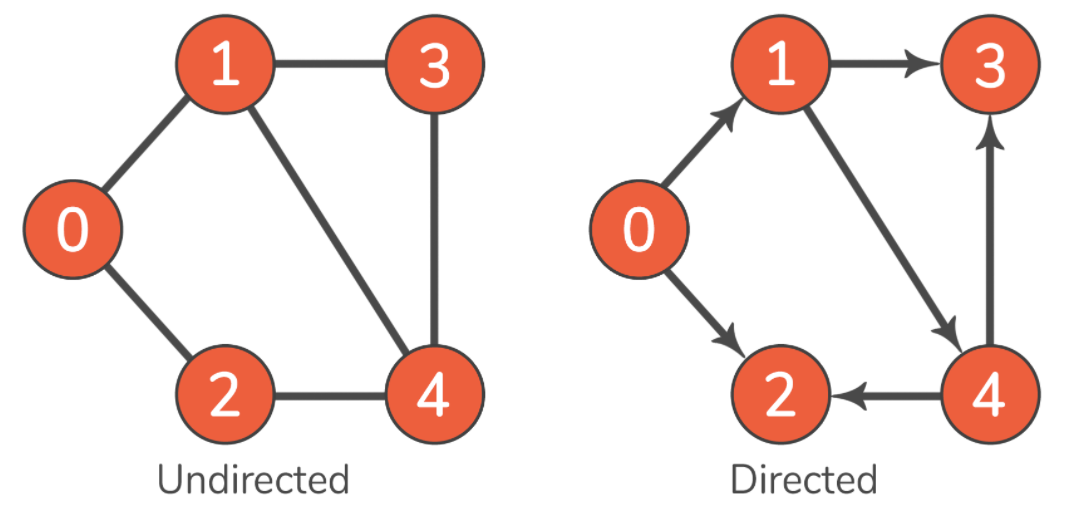

并非图的所有节点都需要与其他节点连接。如果可以从图中的每个节点访问其他任何的节点，我们称该图为连接图(connected)，但有时你通过一些几点无法访问其他节点，那这个图就是未连接图(disconnected)。常见的误解是图的节点之间都必须连接，事实上，图可以不包含边，只有节点：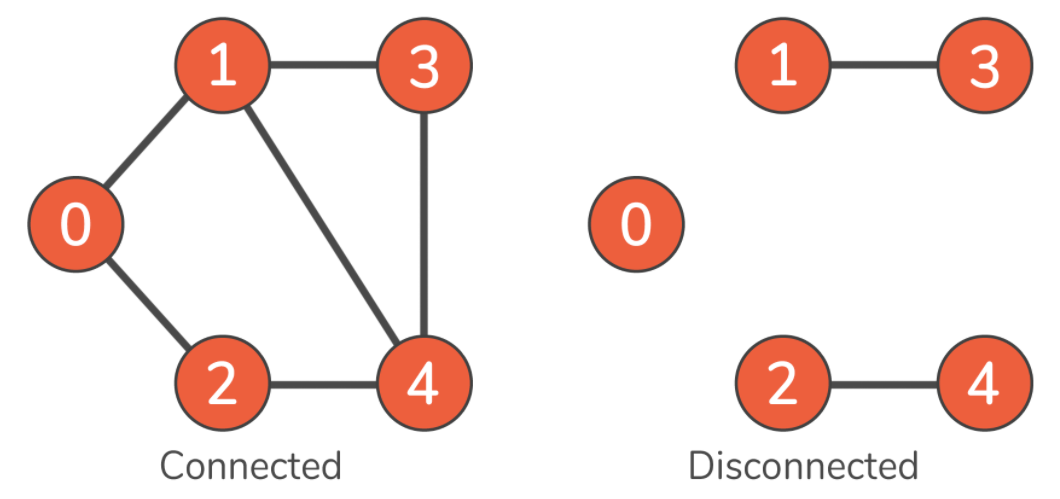

从实现的角度来看，在定义好节点之后，我们需要定义是边缘的权重(weights)。它是分配给边缘的数值，描述了遍历该边缘的成本。边的权重越小，遍历它的成本就越低。基于此，将权重分配给边缘的图称为加权图：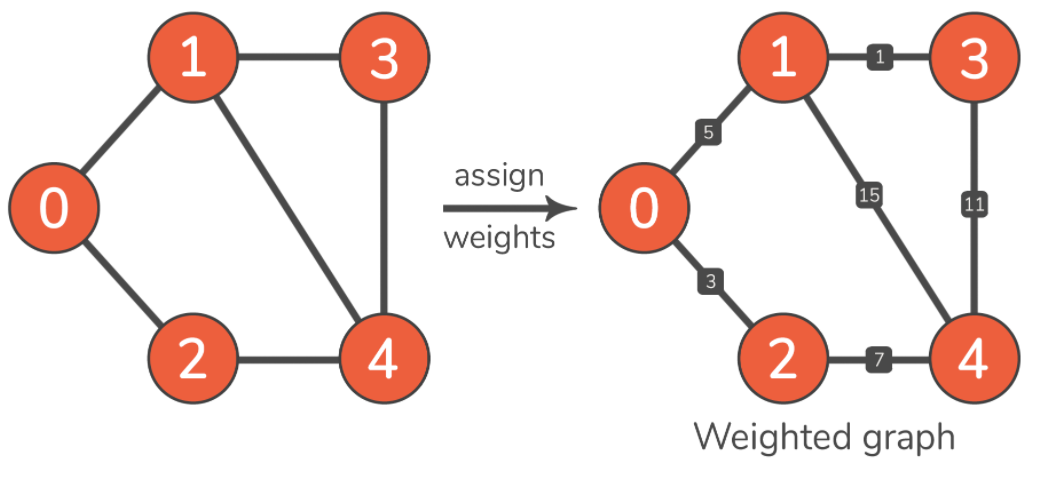

2 图的三种存储方式

一般来说，为了更简单的实现，任何给定图的节点都用数字(从零开始)标记，如果需要字符的方式进行定义节点名称，可用字典的方式进行转换。我将使用以下加权有向图作为后面部分中的示例：

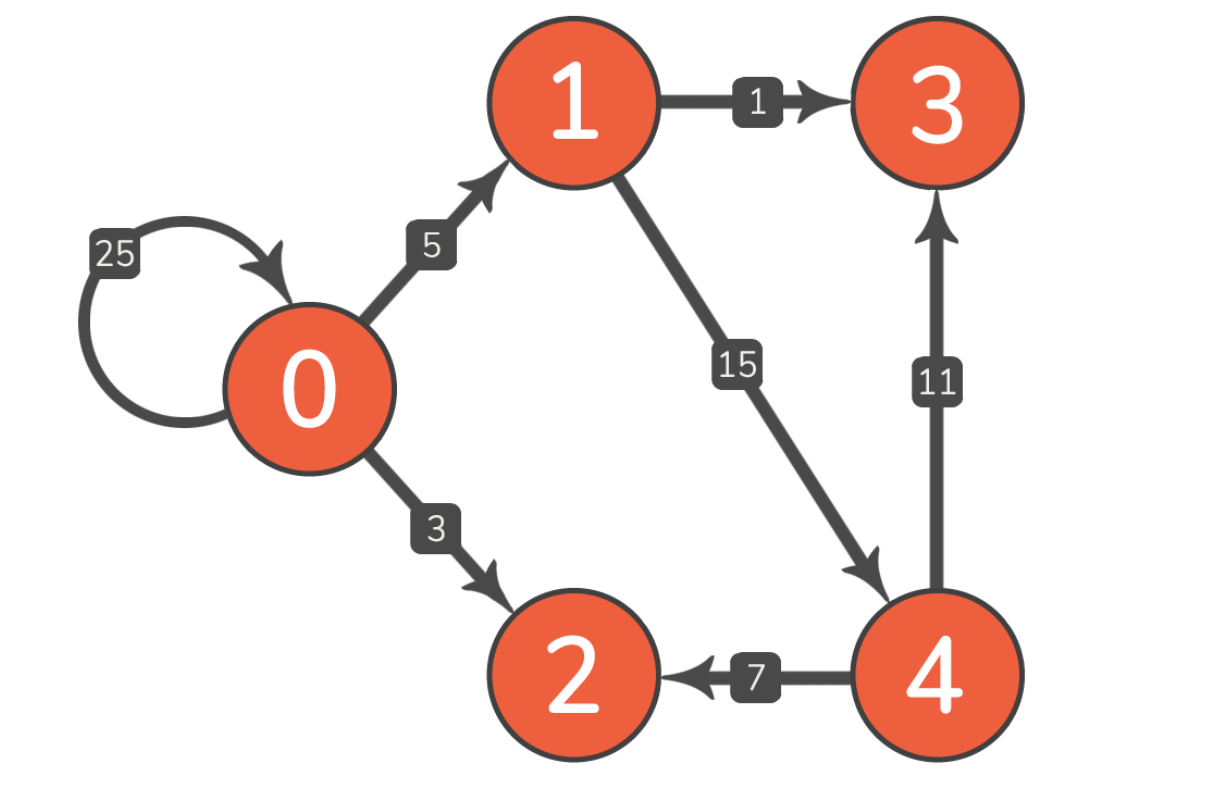
之所以选择加权有向图作为示例，因为它说明了大多数实现的细微差别。一般来说，加权图和未加权图之间的切换非常简单。在有向图和无向图之间切换也是一件非常容易的事情。如果需要，我们将在以下部分中介绍这些主题中的每一个。

2.1 边列表(List of Edges)

2.1.1 原理

边列表是表示图的最简单方法，但由于它缺乏适当的结构，因此通常仅用于说明目的。我们将使用它来解释一些图算法，因为它几乎没有开销，并且允许我们专注于算法实现，而不是图本身的实现。每条边连接两个节点，并且可能分配给它一个权重。因此，每条边都由一个列表以下列方式表示：[node1, node2, weight]，其中 weight 是一个可选属性(如果是未加权的图，则不需要)。顾名思义，边列表将图形存储为以所述方式表示的边列表。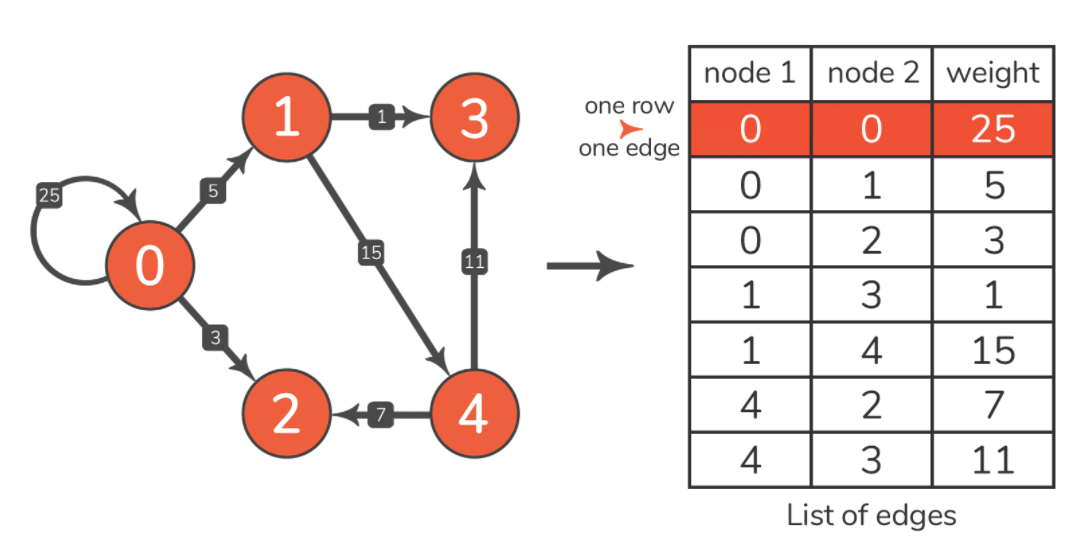
边列表实际上是一张表格。该表的每一行代表一个边，它的两个节点和该边的权重。由于这是一个加权图，边表示中的节点顺序说明了边的方向，即只能从 node1 到 node2 遍历边。在使用边列表处理无向图时，与有向图不同的地方就是权重的定义，有向图定义一个方向，无向图定义两个方向。在下面实现时会详细注释。
优点：

便于实现和理解
非常适合说明目的
按定义表示图(一组节点和一组边)

缺点：

不适合在实际程序中应用
没有使用任何的数据结构进行构造
效率低
不够通用，不能互换地表示有向图和无向图

2.1.2 Python 实现

首先根据边列表的定义编写一个 Graph 类：

class Graph() :
    def __init__(self, num_of_nodes, directed = True):
        self.num_of_nodes = num_of_nodes
        self.directed = directed
        self.list_of_edges = []

    def add_edge(self, node1, node2, weight):
        #从 node1 到 node2 添加权重
        self.list_of_edges.append([node1, node2, weight])

        #如果是无向图，则需要定义 node2 到 node1 的权重
        if not self.directed :
            self.list_of_edges.append([node2, node1, weight])

    #打印边和节点
    def print_edge_list(self):
        num_of_edges = len(self.list_of_edges)
        for i in range(num_of_edges) :
            print(f'Edges : {i + 1} : {self.list_of_edges[i]}')

此实现非常简单，一个图被表示为一个边列表，其中每条边都由一个列表以下列方式表示：[node1, node2, weight]。因此，图实际上是一个矩阵，其中每一行代表一条边。测试：

if __name__ == '__main__':
    graph = Graph(5)

    graph.add_edge(0, 0, 25)
    graph.add_edge(0, 1, 5)
    graph.add_edge(0, 2, 3)
    graph.add_edge(1, 3, 1)
    graph.add_edge(1, 4, 15)
    graph.add_edge(4, 2, 7)
    graph.add_edge(4, 3, 11)

    graph.print_edge_list()

首先，示例图有 5 个节点，因此可以使用构造函数创建一个包含 5 个节点的图。然后将所有边添加到创建的图形并打印图形。这将输出以下内容：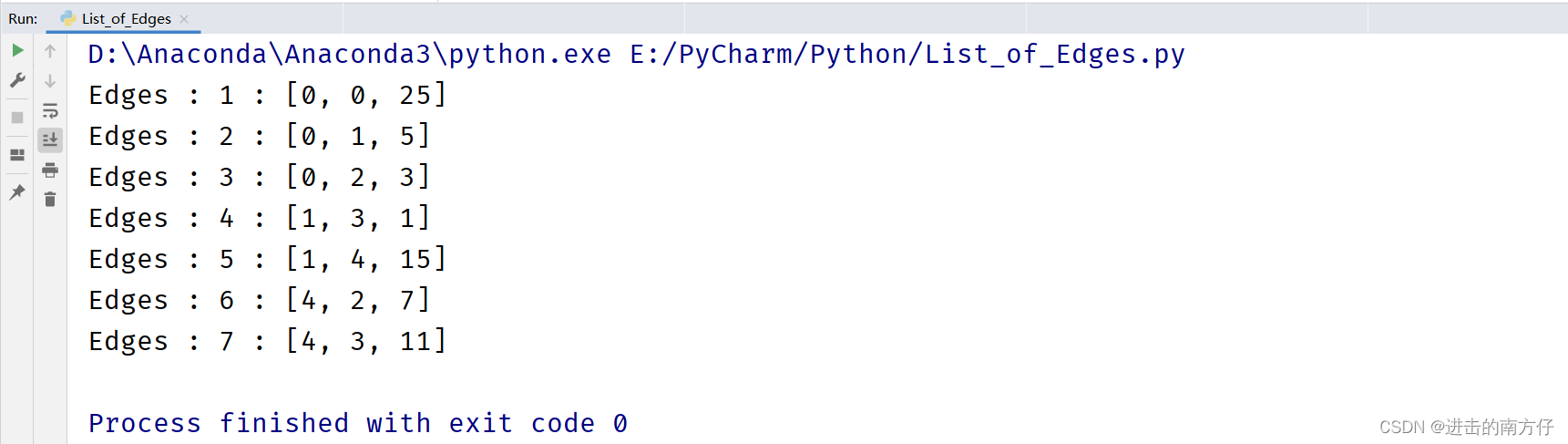

此输出与我们在前几节中显示的边示例列表一致：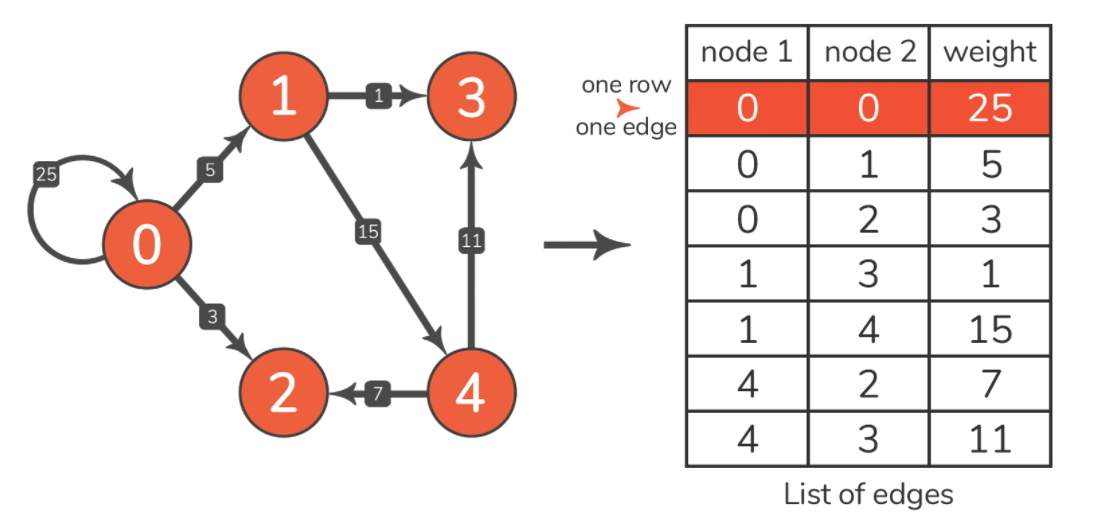

如果想定义无向图，使用 graph = Graph(5, directed = False) 即可。

2.2 邻接矩阵(Adjacency Matrix)

2.2.1 原理

邻接矩阵是表示图的最流行的方法之一，因为它是最容易理解和实现的方法，并且适用于许多应用程序。它使用 nxn 矩阵来表示图( n 是图中的节点数)。换句话说，行数和列数等于图中的节点数。最初，矩阵的每个字段都设置为特殊值 - inf、0、-1、False 等，这表明图中不存在节点。在初始阶段之后，您可以通过填充适当的字段 1(对于未加权图)或边权重(对于加权图)来添加图的每条边。
提到的矩阵本质上是一个表格，每一行和每一列都代表图形的一个节点。例如，下标为 3 的行指的是节点 3，因此可以使用邻接矩阵来仅表示带有编号标记节点的图。第 i 行和第 j 列的值不是初始值则说明节点 i 和 j 之间的边或者权重的存在。邻接图展示如下：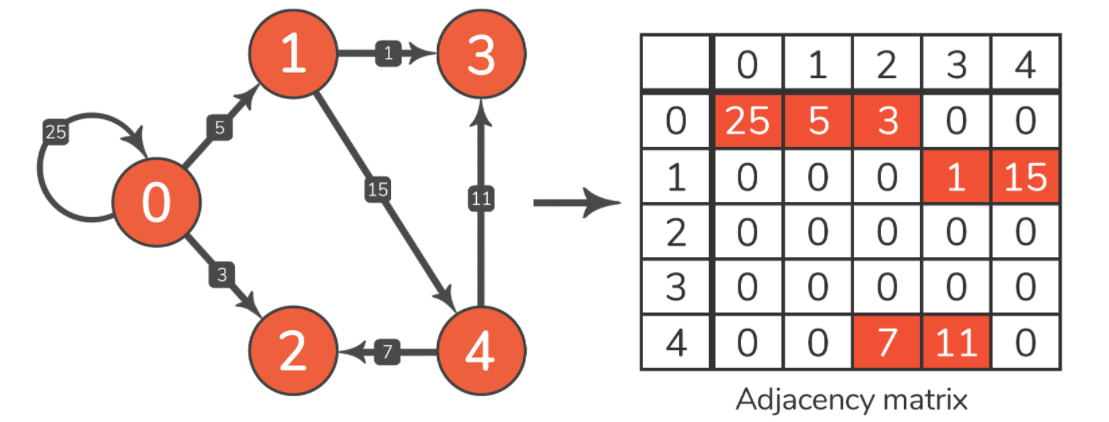

此图中有 n 节点。因此，我们创建了一个包含 n 行和列的表，并将所有单元格初始化为 0，表示任何两个节点之间没有边的特殊值。由于示例图是加权和定向的，因此需要：

遍历图中的每条边
确定该边的开始和结束节点
确定该边的权重
用权重值填充矩阵的适当字段

以边3-4为例。起始节点是 3，结束节点是 4，所以需要填写下标为 [3, 4] 的值。从图像中，可以读取边缘的权重为 11，因此使用填充 11。现在已经标记了边缘的存在 3-4。重复该过程，直到标记了图中的每条边。
优点：

低查找时间，可以在 O(1) 的时间内确定是否存在边
添加/删除边需要 O(1) 时间
便于实现和理解

缺点：

花费更多的空间 O(num_of_nodes²)
添加节点需要 O(num_of_nodes²) 时间
查找所选节点的相邻节点的成本很高 O(num_of_nodes)
遍历图的成本很高 O(num_of_nodes²)
标记/枚举边的成本很高 O(num_of_nodes²)

2.2.2 Python 实现

邻接矩阵本质上是一个简单的 nxn 矩阵，其中 n 是图中的节点数。因此，我们将其实现为具有 num_of_nodes 行和列的矩阵。我们将使用列表推导来构造它并将所有字段初始化为 0。在这种情况下，0 是一个特殊值，指的是图中最初没有边，添加边非常简单：

class Graph():
    def __init__(self, num_of_nodes, directed = True):
        self.num_of_nodes = num_of_nodes
        self.directed = directed
        self.edge_matrix = [[0 for _ in range(num_of_nodes)] for _ in range(num_of_nodes)]

    def add_edge(self, node1, node2, weight):
        self.edge_matrix[node1][node2] = weight

        #无向图
        if not self.directed :
            self.edge_matrix[node2][node1] = weight

    def print_edge_matrix(self):
        for i in range(self.num_of_nodes) :
            print(self.edge_matrix[i])

测试：

if __name__ == '__main__':
    graph = Graph(5)

    graph.add_edge(0, 0, 25)
    graph.add_edge(0, 1, 5)
    graph.add_edge(0, 2, 3)
    graph.add_edge(1, 3, 1)
    graph.add_edge(1, 4, 15)
    graph.add_edge(4, 2, 7)
    graph.add_edge(4, 3, 11)

    graph.print_edge_matrix()

输出：

正如预期的那样，输出与我们在前面展示的矩阵相同：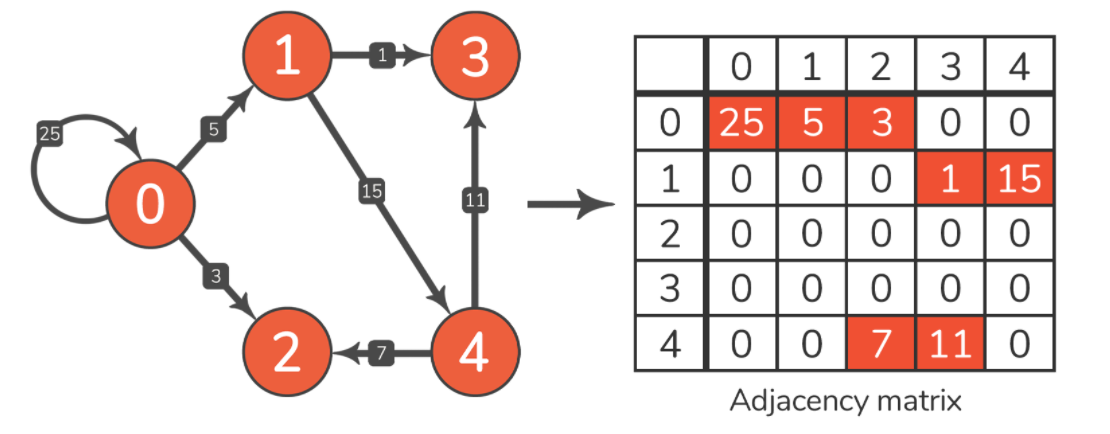

如果想构造无向图，使用以下方式构造函数：graph = Graph(5, directed = False)。

2.3 邻接表(Adjacency List)

2.3.1 原理

邻接表是存储图的最有效方式。它仅存储图中存在的边，这与邻接矩阵相反，邻接矩阵显式存储所有可能的边，包括存在的和不存在的。邻接矩阵最初被开发为仅表示未加权的图，但以最有效的方式是仅使用一个数组来存储一个图。
我们可以仅使用 12 个整数值的数组来表示示例图。将其与邻接矩阵进行比较，邻接矩阵由 n² 元素组成(n 是图中的节点数)，其中邻接列表仅包含 n+e 个元素，其中 n 表示节点数，e 表示图的边的数量。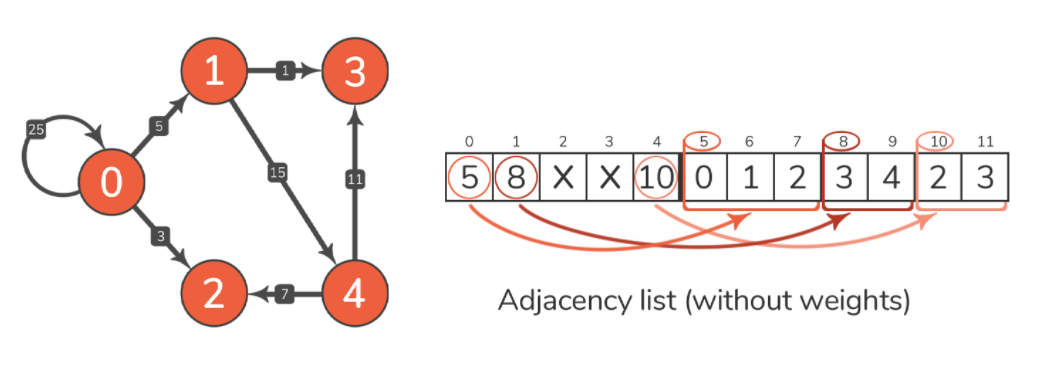

构建邻接表首先需要知道的是图中节点的数量，在示例图中，有 5 个节点，因此列表中的前 5 个位置代表这些节点，比如下标 1 代表第 1 个节点。索引 i 上的值是指列表中的索引，可以在其中找到节点 i 的相邻节点的索引。例如，索引 0 上的值是 5，这意味着应该查看邻接列表中的索引 5 以查找哪些节点连接到节点 0，即节点 0、1 和 2，索引 5 表示邻接节点的开始索引，但是我们怎么知道什么时候应该停止寻找相邻节点？这很简单，查看列表中 0 节点旁边的索引上的值。下一个索引是 1，它代表节点 1，它的值是 8，意思是你可以在邻接表中从索引 8 开始找到与节点 1 相邻的节点。因此，与节点 0 相邻的节点作为索引 5 和 8 之间列表的值。
为了更容易理解这种结构，可以以更结构化的方式重新排列邻接列表的元素。如果这样做，就会看到生成的结构看起来很像一个链表：

此外，链表的结构与字典非常相似。它有一组键(节点)，以及每个键的一组值(一组与键节点相邻的节点)。如果要表示加权图，则必须找到一种在相邻节点之外存储权重的方法（如下图所示）。下图显示了示例图的邻接列表包括有和没有权重：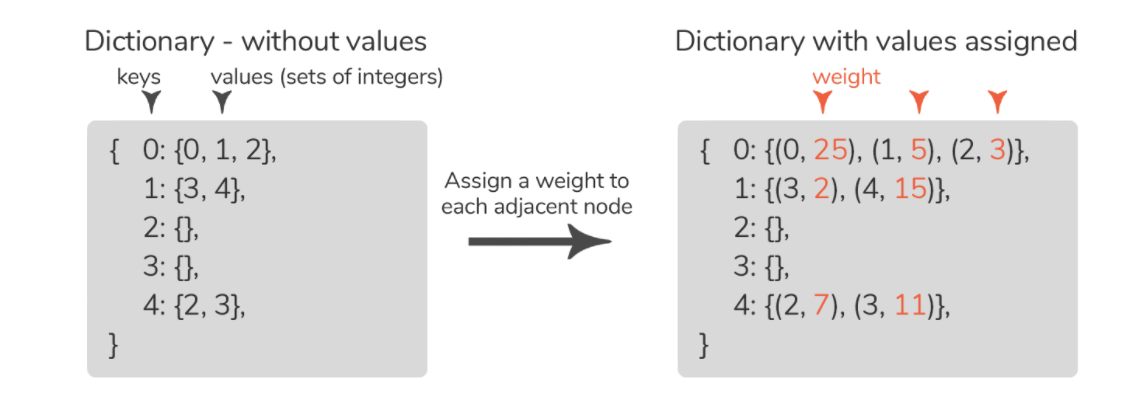

当查看加权相邻列表时，可以轻松构建示例图的边集。节点 0 具有三个相邻节点：0、1、2，这意味着图具有边 0-0、0-1 和 0-2。这些边的权重也可以从邻接表中读取，边 0-0 的权重为 25，边 0-1 的权重为 5，依此类推。
优点：

快速地找到所选节点的相邻节点 O(1)
对密度较低的图有效(与节点数相比，边数较少)
可以将它用于字母和数字标记的节点
遍历图的成本低 O(length_of_list)，length_of_list 长度等于图中节点数和边数之和
标记/枚举边的成本低 O(length_of_list)

缺点：

查找花费时间多 O(length_of_list)
移除边的成本高 O(length_of_list)

2.3.2 Python 实现

正如我们在前面所解释的，在 Python 中表示邻接列表的最佳方式是使用字典——它具有一组键和对应的值。我们将为每个节点创建一个键，并为每个键创建一组相邻节点。这样，我们将有效地为图中的每个节点创建一组相邻节点。本质上，相邻节点代表关键节点和相邻节点之间的边，因此我们需要为每条边分配权重。因此要将每个相邻节点表示为一个元组：一对相邻节点的名称和该边的权重：

class Graph() :
    def __init__(self, num_of_nodes, directed = True):
        self.num_of_nodes = num_of_nodes
        self.directed = directed
        self.adjacency_list = {node : set() for node in range(num_of_nodes)}

    def add_edge(self, node1, node2, weight):
        self.adjacency_list[node1].add((node2, weight))

        #无向图
        if not self.directed :
            self.adjacency_list[node2].add((node1, weight))

    def print_adj_list(self):
        for key in self.adjacency_list.keys() :
            print(f'node {key} : {self.adjacency_list[key]}')

测试：

if __name__ == '__main__':
    graph = Graph(5)

    graph.add_edge(0, 0, 25)
    graph.add_edge(0, 1, 5)
    graph.add_edge(0, 2, 3)
    graph.add_edge(1, 3, 1)
    graph.add_edge(1, 4, 15)
    graph.add_edge(4, 2, 7)
    graph.add_edge(4, 3, 11)

    graph.print_adj_list()

输出：
输出与前面描述的链表和字典相同：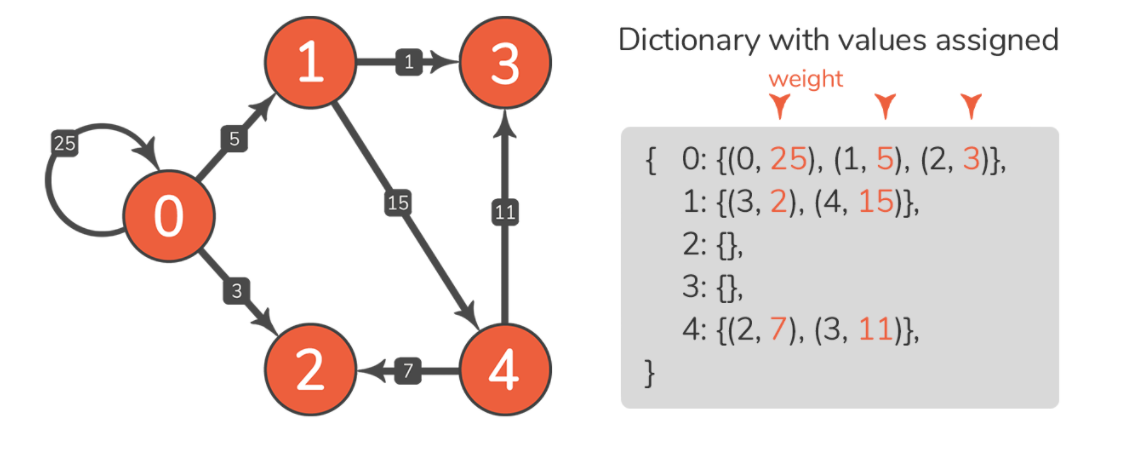

如果想构造无向图，使用以下方式构造函数：graph = Graph(5, directed = False)。

Z.H.Chen's Blog

Python 中的图：图的存储结构

1 什么是图

2 图的三种存储方式

2.1 边列表(List of Edges)

2.1.1 原理

2.1.2 Python 实现

2.2 邻接矩阵(Adjacency Matrix)

2.2.1 原理

2.2.2 Python 实现

2.3 邻接表(Adjacency List)

2.3.1 原理

2.3.2 Python 实现